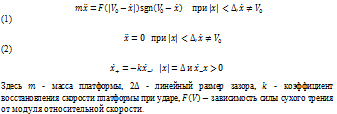Аннотация
Введение
1.Описание модели
2.Периодические движения изучаемой системы
3.Исследование периодических движений с состоянием относительного покоя платформы и плиты
4.Исследование периодических движений , в которых в определенные промежутки времени имеет место относительный покой платформы плиты
5.Коэффициент восстановления скорости
6.Исследование фазовой плоскости
7.Частота фрикционных автоколебаний
8.Заключение
Список литературы
Автоколебания – незатухающие колебания в диссипативных нелинейных системах, которые поддерживаются за счет внешнего источника энергии. Вид и свойства этих колебаний (частота, амплитуда, форма) определяются самой системой и не зависят от начальных условий. Характерная особенность автоколебаний – отсутствие внешнего периодического воздействия.
Схематично автоколебательную систему можно представить в виде источника энергии, осциллятора с затуханием и обратной связи (нелинейного элемента) .
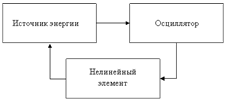
Схематичное изображение автоколебательной системы
Осциллятор сам регулирует поступление энергии от внешнего источника, что отличает автоколебания от вынужденных колебаний, когда внешний источник определяет, когда и сколько энергии передать осциллятору, задавая тем самым частоту, амплитуду, фазу и форму колебаний. При автоколебаниях, благодаря наличию нелинейного элемента обеспечивается согласование подачи энергии с работой осциллятора. Автоколебания окружают нас повсюду в природе и технике: часы, звучащая скрипичная струна или органная труба, бьющееся сердце – все эти системы совершают автоколебания.
Особого внимания заслуживают механические автоколебания, возникающие в системах с трением. Сила трения, которая в некоторых моделях оказывалась причиной затухания колебаний, может явиться причиной их раскачивания.
Одним из примеров таких автоколебаний являются фрикционные – автоколебания возникающие в системах с нелинейным трением.
ОПИСАНИЕ МОДЕЛИ
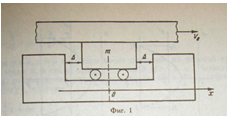
Рассмотрим следующую механическую систему: к платформе массы способной перемещаться в прямоугольном зазоре с твердыми стенками, в некоторый момент времени прижимают плиту, движущуюся с постоянной скоростью (рис.1).
Математическая модель этой механической системы описывается дифференциальным уравнением второго порядка с соответствующими граничными условиями:
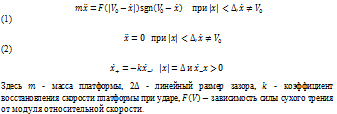
- . БаландинД.В Фрикционные автоколебания в зазоре. Известия Российской академии наук. Механика твердого тела. 1993. № 1. С. 54.
- 2.Крагельский И. В., Гитис Н. В. Фрикционные автоколебания. М.: Наука, 1987. 183 с.
- 3.Нагаев Р. Ф., Сарафян Г. С. Фрикционные автоколебания в системе кусочно-линейной характеристики трения // Прикл. Механика. 1990. Т. 26, № 10. С. 84-90.
- 4.Jan Awrejcewicz, Yuriy Pyryev. Dynamics of a two-degrees-of-freedom system with friction and heat generation. Communications in Nonlinear Science and Numerical Simulation 11 (2006) 635-645/