ВКР Моделирование процессов сцепления арматуры и бетона

Быстрое развитие технологий и применения новых материалов в строительной отрасли ставит перед инженерами новые задачи, требующие обеспечения более жестких стандартов по производственным и эксплуатационным характеристикам. Снижение стоимости возведения, эксплуатации и межремонтного периода требует применения новых и инновационных видов строительных материалов и технологий

В XX веке железобетон зарекомендовал себя, как один из лучших материалов для строительства, более 90 процентов всех конструкций возводятся именно из железобетона. Он обладает высокими прочностными характеристиками, большим сроком службы и сравнительно небольшой ценой, поэтому зачастую является экономически выгодным при устройстве строительных конструкций.

Известно, что взаимодействие бетона и арматуры, как единого целого происходит за счёт трёх факторов [1]: механическое зацепление арматуры за бетон, при наличии неровностей на поверхности арматуры, трение между бетоном и арматурой, молекулярное взаимодействие (адгезия). Описание сложного многопараметрического взаимодействия бетона и композитной арматуры характеризует кривая зависимости «напряжения сцепления – проскальзывание арматуры относительно бетона», или альтернативная зависимость «выдергивающая сила – проскальзывание арматуры относительно бетона» [2-4]. Построить такую кривую можно используя экспериментальный метод выдергивания стержня из куба (Pull-outtest) согласно RILEM/CEB/FIB [2, 5].

В работе обосновывается актуальность построения новых моделей взаимодействия бетоны и арматуры, приводятся основные положения метода конечных элементов     , реализована методика конечно-элементного расчета деформирования железобетонной конструкции с учетом отрыва арматуры от бетона, проведен расчет процесса «вырыва» прута арматуры из бетонного образца, проведен анализ полученных результатов.

Глава 1. Расчет армируемых конструкций

Известно 7 классов моделей сцепления бетона и арматуры [1]:

- модель идеального сцепление арматуры и бетона;

- модель с добавлением дополнительного слоя с пониженным модулем деформации;

- модель с использованием связей с конечной жесткостью;

- модель с выключением разрушенных элементов из работы;

- модель с учётом микрорастрескивания;

- модель упруго-поврежденного материала;

- модель упруго – пластично – поврежденного материала.

Наибольшее распространение получили три первых модели, остальные модели требуют наличия программных комплексов высокого уровня, как ANSYS, Nastran, ABAQUS и другие.

Модель идеального сцепления арматуры и бетона не учитывает несплошность среды и микрорастрескивание, однако широко и повсеместно используется в численных расчётах железобетонных элементов, так как потеря несущей способности арматуры достигается быстрее, чем утрачивается сцепление между арматурой и бетоном.

Модель с добавлением дополнительного слоя с пониженным начальным модулем деформации, требует более подробной дискретизации расчетной модели, а именно применения объемных конечных элементов с мелкой разбивкой сетки для бетона, арматуры и самого граничного слоя, что не позволительно для расчёта сложных расчётных схем, так как потребует больших временных затрат.

Модель, основанная на использовании связей с конечной жесткостью, считается наиболее логичной, а также имеет наибольшую согласованность с экспериментальными и теоретическими результатами сцепления металлической арматуры с бетоном [1]. Данная модель позволяет учитывать нелинейные смещения арматуры относительно бетона в процессе разрушения связей сцепления. Для численного описания модели требуется вводить дополнительные элементы с конечной жёсткостью или по-другому податливые связи.

Авторами [6] предлагаются для использования нелинейные пружины, свойства которых описываются по диаграммам сцепления арматуры с бетоном. Не во всех расчётных комплексах доступен данный тип КЭ, поэтому необходимо упростить модель, а именно нелинейные пружины следует заменить линейными пружинами с предельным усилием на растяжение или сжатие. Тогда для аппроксимации нелинейной диаграммы сцепления арматуры[7, 8], с бетоном, представленного на графике 1 (рисунок 1) предлагается использовать кусочно-линейную функцию, изображенную на графике 2 (рисунок 1), которая описывается формулой:

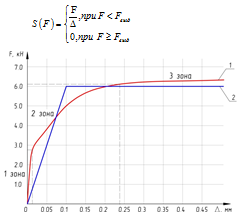
Рис. 1. Графики зависимости перемещения стеклопластиковой арматуры Δ от выдергивающей силы F, 1 – по результатам испытаний; 2 – для численного моделирования.

1. БенинА.В., Семенов А.С., Семенов С.Г., Мельников Б.Е. Математическое моделирование процесса разрушения сцепления бетона с арматурой. Часть 1. Модели с учётом несплошности соединения // Инженерно - строительный журнал. 2013. №5. С. 86 – 99.
2. ГОСТ 31938-2012 Арматура композитная для армирования бетонных конструкций. Общие технические условия. М.: Изд. Стандартинформ, 2014. – 35 с.
3. Климов Ю.А., Солдатенко О.С., Орешкин Д.А.Экспериментальные исследования композитной неметаллической арматуры с бетоном // URL: http://www.ekibar.org/files/frp_rebar_test_adhesion_concrete.pdf (10.03.2015).
4. Бенин А.В., Семенов С.Г. Экспериментальные исследования сцепления композитной арматуры с плоской навивкой с бетоном // ПГС. 2013. №9/2013. С 74-76.
5. RILEM/CEB/FIB Recommendation on reinforcement steel for reinforced concrete. RC6. Bond test for reinforcement steel. 2. Pull-out tests. 1983. 8 p.
6. Хозин В.Г., Гизатуллин А.Р., Куклин А.Н., Пискунов А.А. Сцепление полимеркомпозитной арматуры с цементным бетоном // Известия КГАСУ. №1 (23). С.211-213.
7. Пискунов А.А., Зиннуров Т.А., Бережной Д.В., Умаров Б.Ш., Вольтер А.Р. О результатах экспериментального и численного исследований напряженно-деформированного состояния бетонных конструкций, армированных предварительно напряженными полимеркомпозитными стержнями // Транспортные сооружения, 2018 №2, https://t-s.today/PDF/02SATSpdf
8. Zinnurov T.A., Piskunov A.A., Safiyulina L.G., Petropavlovskih O.K., Yakovlev D.G., Berezhnoi D.V. and Balafendieva I.S. Numerical modeling of composite reinforcement with concrete // Journal of Physics: Conference Series, 2019, Vol.1158, 042046
9. Зенкевич О. Метод конечных элементов в технике. – М. : Мир, 1975. – 541 с.
10. Голованов А.И., Бережной Д.В. Метод конечных элементов в механике деформируемых твердых тел. – Казань,-2001.- 301с.
11. Образцов И.Ф., Савельев Л.М., Хазаков Х.С. Метод конечных элементов в задачах строительной механики летательных аппаратов. - М. :Высшая школа , 1985.–329 с.